¶ 7, 8, & 9: Introduction: My Grand Narrative: Slouching Towards Utopia: Notes & Long Notes
I am starting to go through the manuscript of my forthcoming book, paragraph-by-paragraph, adding in the full notes that could not make it into the print version...
¶ 7, 8, & 9: Things changed starting around 1870. Then we got the institutions for organization and research and the technologies—we got full globalization, the industrial research laboratory, and the modern corporation.[n] These were the keys. These unlocked the gate that had previously kept humanity in dire poverty. The problem of making humanity rich could now be posed to the market economy, because it now had a solution. On the other side of the gate, the trail to utopia came into view. And everything else good should have followed from that.
Much good did follow from that.
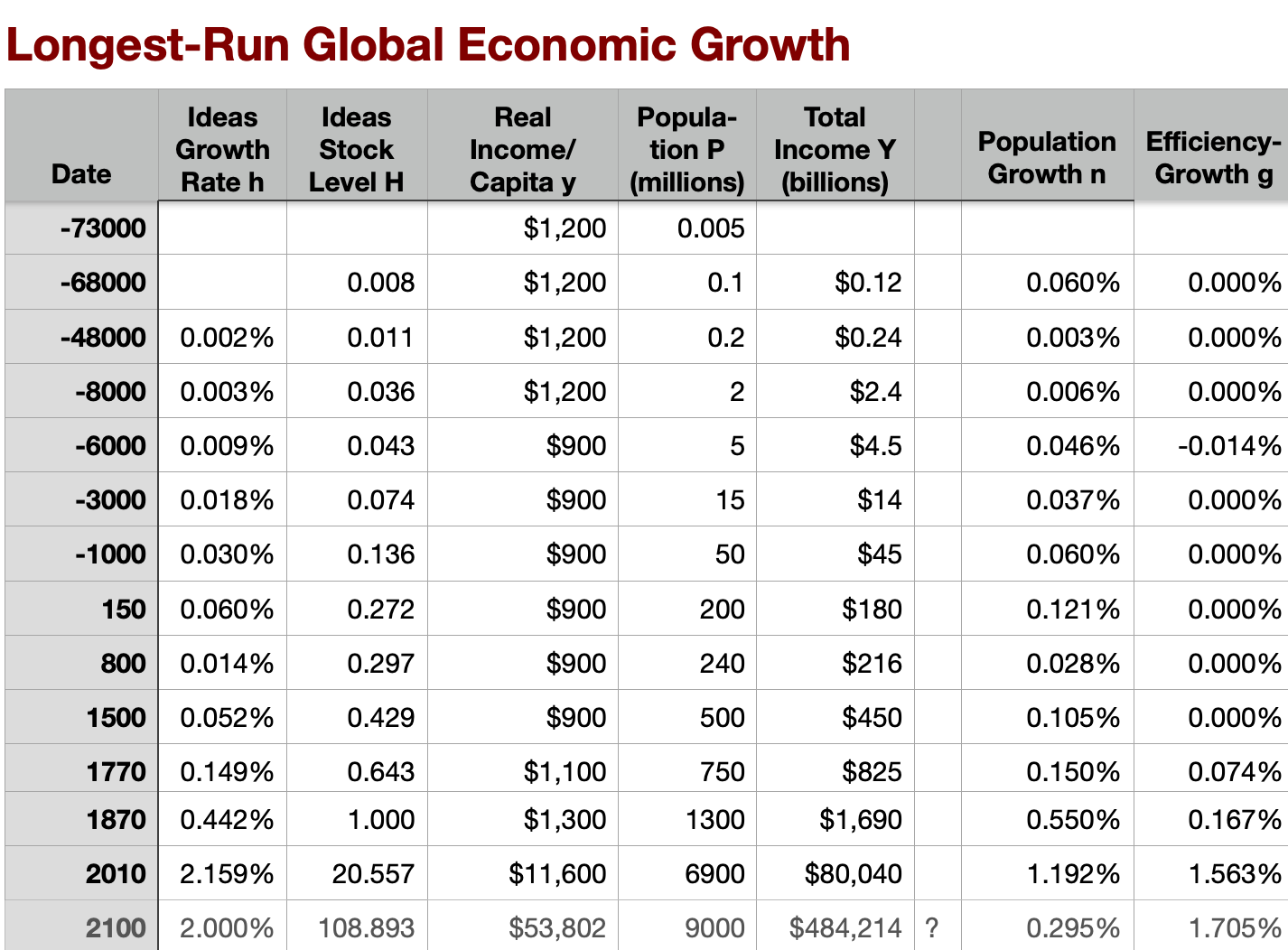
My estimate—or perhaps my very crude personal guess—of the average worldwide pace of what is at the core of humanity’s economic growth, the proportional rate of growth of my index of the value of the stock of useful ideas about manipulating nature and organizing humans that were discovered, developed, and deployed into the world economy, shot up from about 0.45 percent per year before 1870 to 2.1 percent per year afterward, truly a watershed-boundary crossing difference. A 2.1 percent average growth for the 140 years from 1870 to 2010 is a multiplication by a factor of 21.5. That was very good: the growing power to create wealth and earn an income allowed humans to have more of the good things, the necessities, conveniences, and luxuries of life, and to better provide for themselves and their families. This does not mean that humanity in 2010 was 21.5 times as rich in material-welfare terms as it had been in 1870: there were six times as many people in 2010 as there were in 1870, and the resulting increase in resource scarcity would take away from human living standards and labor-productivity levels. As a rough guess, average world income per capita in 2010 would be 8.8 times what it was in 1870, meaning an average income per capita in 2010 of perhaps $11,000 per year. (To get the figure of 8.8, you divide 21.5 by the square root of 6.) Hold these figures in your head as a very rough guide to the amount by which humanity was richer in 2010 than it was in 1870—and never forget that the riches were vastly more unequally distributed around the globe in 2010 than they were in 1870.[6][o]
Printed Endnotes:
[6] The growth and international inequality numbers are very disputable and are often disputed. To gain a sense of what the current semi-consensus is, see: Hans Rosling et al., Gapminder, <http://gapminder.org>; Max Roser et al., Our World in Data, https://ourworldindata.org/grapher/globalization-over-5-centuries?country=~OWID_WRL
Longer Notes:
[n] There should be a chapter, or at least an essay, on the coming of the Second Industrial Revolution, its component pieces, and their impact. I regret I have not (yet) managed to write it. I observe the Global North and worldwide speedups in growth around 1870; I see the tremendous increase brought by modern full globalization in the incentives to discover, develop, deploy, and via copying the example of others diffuse the fruits of science and technology . I observe the rationalization and routinization of the processes of discovery and development on the one hand and of development and deployment on the other brought by the coming of the industrial research lab and the modern corporation. But I have not yet found a good summary essay to point to.
[o] In the aggregate growth-modeling tradition that has developed from Robert Solow, “A Contribution to the Theory of Economic Growth”, Quarterly Journal of Economics, Vol. 70, No. 1 (Feb., 1956), pp. 65-94 <https://www.jstor.org/stable/1884513>, the level of real net output per worker Y/L, with Y for net output and L for the labor force, is a simple mathematical function of the capital-intensity of the economy K/Y, of how much of produced means-of-production K per unit of net output there is assisting workers in creating that output per worker; and of the efficiency of labor E:
Y/L = (K/Y)^(⍺/(1-⍺)) E
Such an economy will tend to converge to a steady-state growth path in which the capital intensity K/Y approaches its steady-state value (K/Y)* given by:
(K/Y)^* = s/(n+g)
Where s is the net savings-investment rate of the economy, n is the proportional rate of growth of the labor force L, and g is the proportional rate of growth of labor efficiency E. (Yes: you usually see this equation with a “δ” in the denominator for the depreciation rate on capital, and with Y defined not as net but gross output, and with s defined as the gross savings rate out of gross output. But—as Solow pointed out to me, and has Piketty has stressed—while there is reason to think that having people save a constant proportion of their net output is a reasonable baseline case to start from, there is no reason to think that people save a constant proportion of their gross output—that net savings would be less in an otherwise-identical economy where capital equipment just happened to be less durable.)
The efficiency of labor E can then be thought of as a function of the level of knowledge about “technology” H—discovered, developed, and deployed ideas about manipulating nature and organizing humans—and of resources per worker R/L, where more resources per worker allow humans to be more productive, and where increasing resource scarcity leads to a fall in net output per worker Y/L unless there are countervailing improvements in knowledge:
E = H (R/L)^ƛ
When natural resources are constant—as they are for the world economy as a whole, although not for individual sub civilizations—this means that the proportional growth rate of the efficiency of labor is:
g = h - ƛn
If we assume that the world economy’s steady-state capital-output ratio is constant across and within eras of economic growth, then the rate of growth of output per worker g_Y/L will be the same as the rate of growth of the efficiency of labor g. We can then read what the proportional rate of growth of knowledge about technology h from the rate of growth of average labor productivity and the rate of growth of the global labor force:
h = g_Y/L + ƛn
I assume ƛ=1/2. Why? If ƛ=0, we are assuming that resource scarcity is simply not a thing: that at a given level of technological knowledge standards of living are independent of how large average firms are and how many workers are drawing on the same metal deposits. If ƛ=1, we are assuming that labor is simply unproductive: that total output depends only on the level of technological knowledge H and the level of natural resources R, with a doubling of the labor force leading to a halving of labor productivity. Both of those are clearly wrong. Halfway between seems to me a not-unreasonable baseline.
Alternative calculations are easy to do if you have a different sense of how important resource scarcity is as a binding or as a not-very-binding constraint on human economies.
There are near-consensus guesses as to the average level of net output per worker and the size of the human population since deep time. Under the further assumption that the effective labor force is a constant share of the human population—that as the share of the population too young to work has fallen, the share that is retired has risen to approximately offset—the rate of labor-force growth is the same as the rate of population growth. And thus I can calculate my guesstimates of the rate of growth of h.