A very nice piece from Rafael Guthmann. But I do have a quibble:
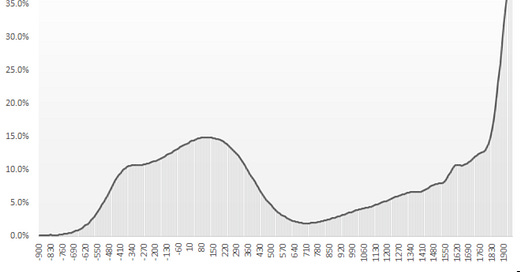
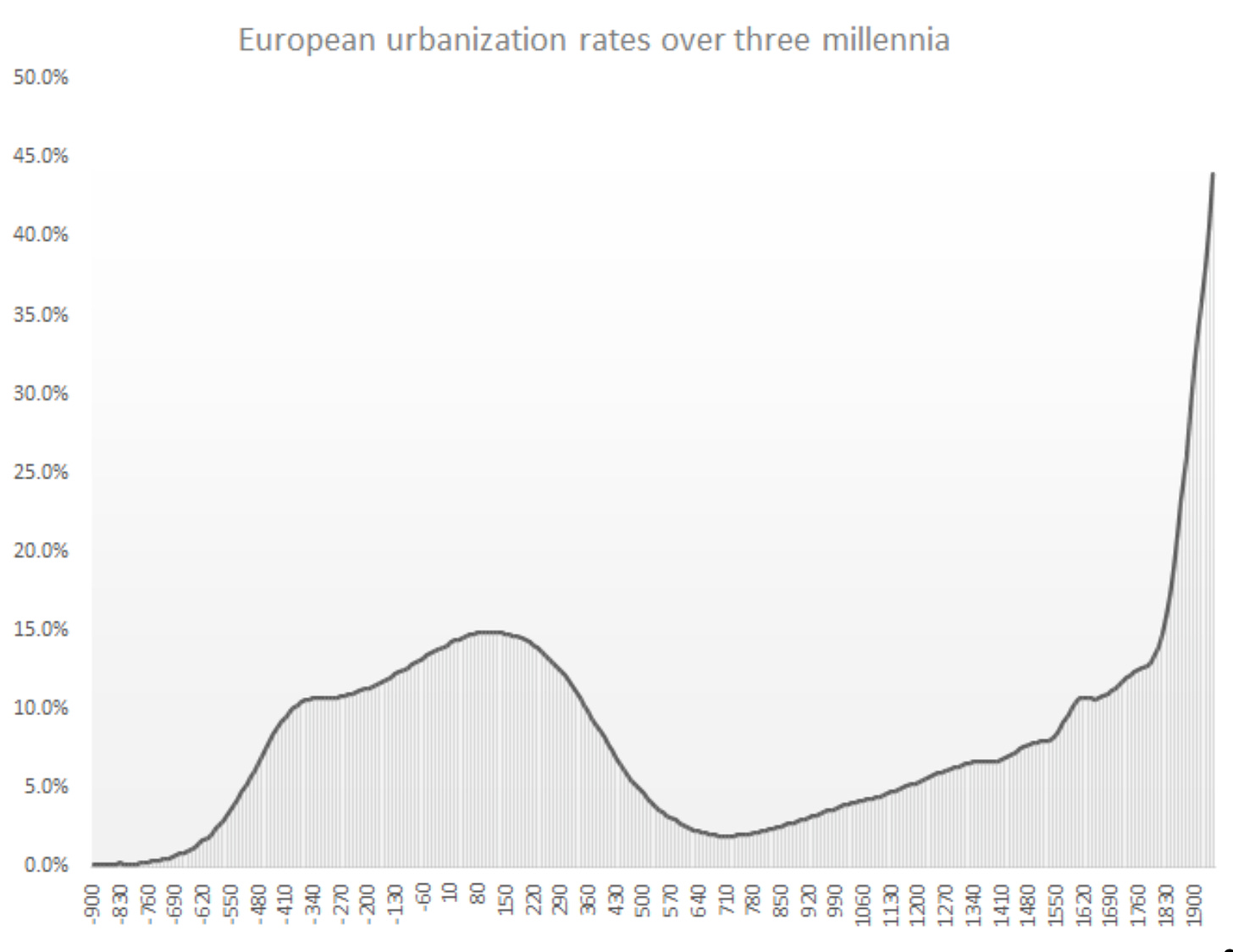
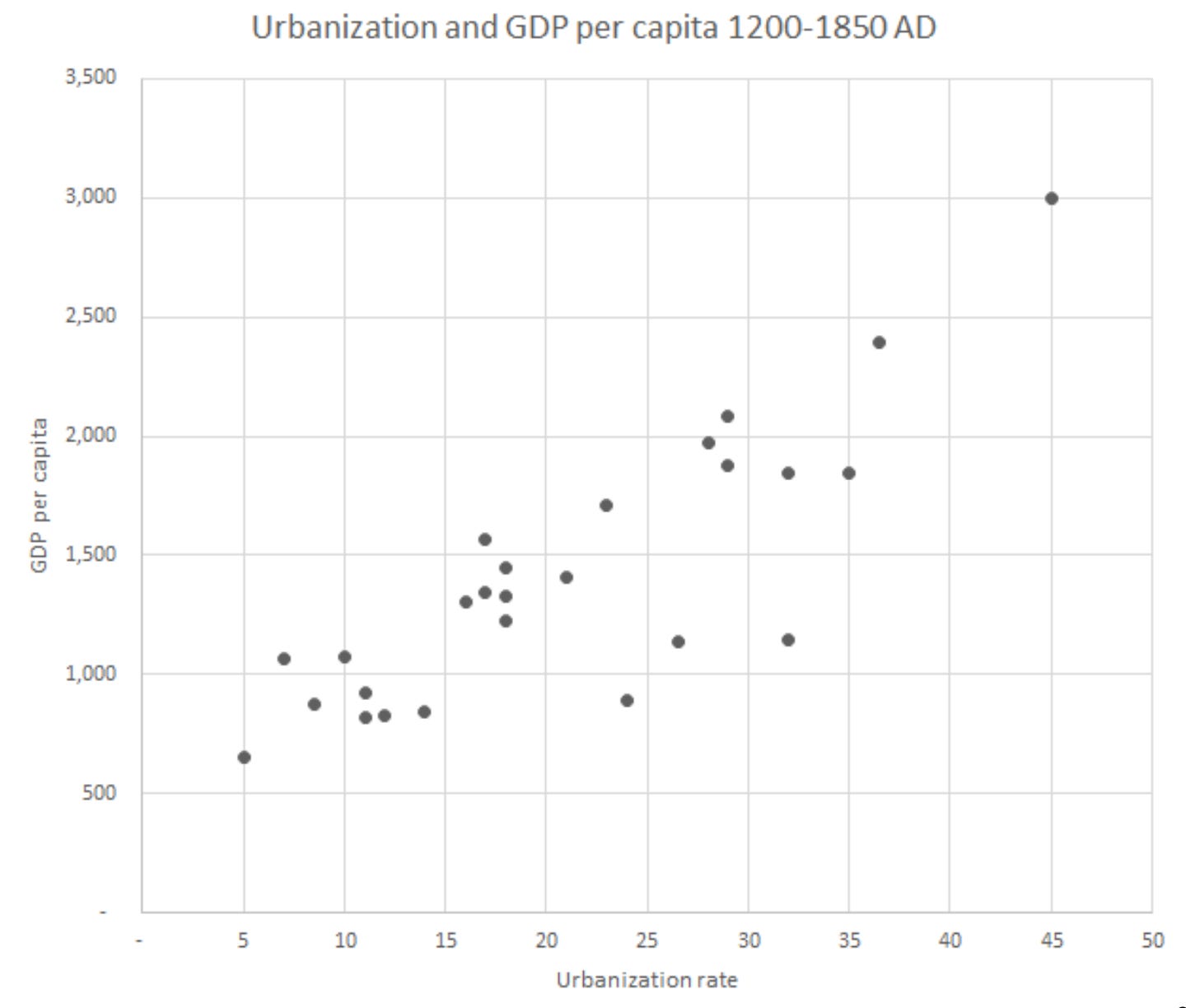
Rafael R. Guthmann: The Malthusian Trap Never Existed: ‘From… Buringh (2021), and Bairoch and Goertz (1986), I estimated Europe’s urban population… and dividing by the estimated population of Europe over the past 3,000 years we get the following… a much more nuanced and interesting trajectory of macroeconomic performance for Europe than the Malthusian-trap model…. It also shows that there was slow progress upwards from the 8th century to the 18th century, roughly at 10% of the urbanization growth rate in the 19th and 20th centuries. The decline and fall of the Roman Empire from the 2nd century to the 7th century is also clear… the greatest sustained process of economic regression in human history…. The economic flourishing of Classical Greece and other parts of the European Mediterranean from the 9th… century BC appear to have constituted the fastest period of economic growth in Europe until the late–18th century….
The urbanization rate suggests that over the last three millennia of the history of Europe, there were long and sustained periods of economic progress and regression and that modern economic growth has been a dramatic acceleration compared to the pre-modern trend, instead of a complete break from it…
My quibble: I think it unwise to call these pre-1750 régimes “non-Malthusian” in any profound sense.
Let us build a Solow-Malthus model. Let us start by saying there is technology—the discovered, developed, deployed, and diffused set of useful ideas about manipulating nature and organizing humans to make us more productive. Let us call the level of technology H. Let's also say that there is a population/labor force L—no real reason to distinguish between them. And let us also say that there is an efficiency of labor E, conceptually different from technology because of the impact of resource abundance or scarcity on labor efficiency. And let us use h, n, and g for the proportional growth rates of H, L, and E:
Let us then say that the level of output per worker or per capita—again, no great reason to distinguish sharply between them—y is determined by the economy’s capital-intensity 𝜅, the salience of capital in production θ, and labor efficiency E. And let us remember that in Bob Solow’s standard model the equilibrium (for which we will use *) level of capital intensity 𝜅 is equal to the economy’s savings-investment rate s divided by its investment requirements, which are the sum of the labor-efficiency growth rate g, the labor-force growth rate n, and the depreciation rate δ. (Yes, I know, I know: it makes no conceptual sense to assume that people’s gross savings is a constant share of gross production because they never take any account of the changing relative wedge between gross and net production. I asked Bob Solow about this once. He shrugged and said: referees. We use the consensus models we have.)
Now let us make the model Malthusian. Let us say that the growth rate of labor efficiency g is equal to the growth rate of the useful-ideas stock h minus the labor-force growth rate n divided by the salience ɣ of ideas in labor efficiency. Why? Because a higher labor force induces resource scarcity which is a drag on labor efficiency. And let us now compare the level of output per capita y to some “subsistence” level of necessities consumption y^sub times some allowance for “luxuries” φ. When production per capita is such that after allowing for luxuries necessities consumption is greater than subsistence, the population grows, with β capturing how much extra population growth is induced by a given wedge between necessities consumption and subsistence:
This is a thoroughly Malthusian model. We can see immediately that it has an equilibrium balanced growth path at which capital intensity and productivity are at their equilibrium values and the population and labor force are growing at the rate warranted by the rate of ideas growth and the salience of ideas in generating labor efficiency:
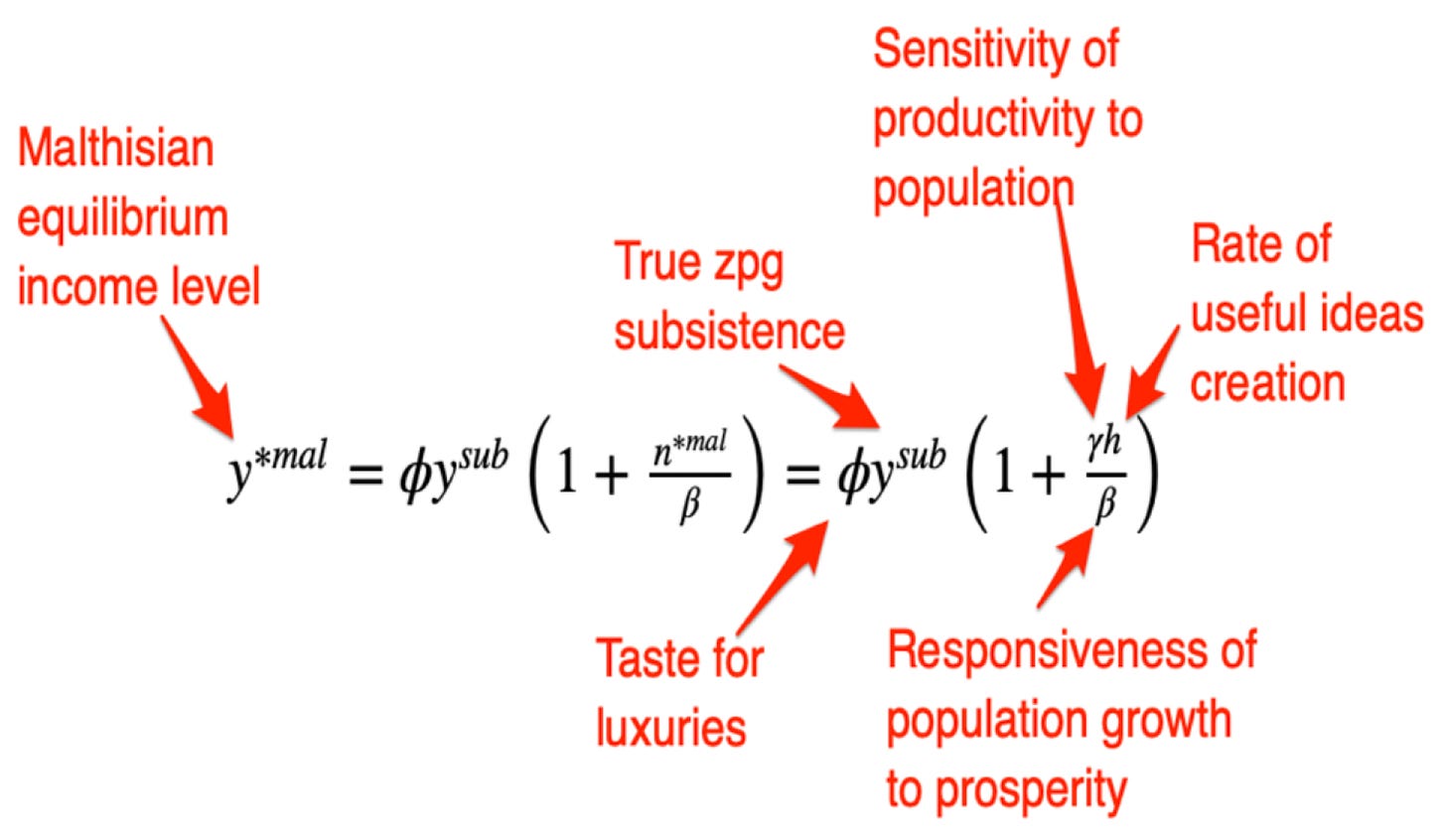
If we crank through the algebra, we can see that this model’s equilibrium is rather rich. Along the equilibrium balanced-growth path, we have equilibrium income per capita:
And equilibrium population:
In this model, the most important determinants of the equilibrium level of income per capita are the society’s taste for luxuries multiplied by its level of “subsistence” necessities consumption. Both of these are profoundly socio-economic factors, potentially different for different societies and potentially changing over time. How much of its productivity society diverts from making commodities directly useful for boosting nutrition and reproductive fitness and, instead, devotes to conveniences and luxuries—including the "luxuries" of having an upper class, and the “super-luxury” of living in cities and gaining all the conveniences and benefits of urban life at the cost of making itself more vulnerable to plague and disease—are not biological factors fixed in stone but are instead the result of a society’s sociology, economic structure, and politics. What a society’s level of “subsistence” necessities consumption happens to be is itself as much a sociological as a biological fact. At what age do women become sexually active? Is female infanticide a thing, and if so how much of a thing? Does the society’s—or do the societies’—social practice of war involve mass sacrifice of captives to gods, or routinely carving the blood eagle, or chevauchée?,
In this model, the most important determinants of the equilibrium level of population relative to resources are (a) the current level of the value of the ideas stock H divided by subsistence necessities consumption, the economy’s savings-investment share s divided by the depreciation rate δ, (c) the salience θ of capital in generating production, (d) the (inverse of the) taste for “luxuries” φ, all raised to the power ɣ that is the salience of ideas vis-à-vis resources in generating labor efficiency. As known above, the “taste” for “luxuries” is in no wise a matter of biology, and the level of “subsistence” necessities consumption only partially so. In the equilibrium-population equation, moreover, the economy’s savings-investment share of production is also a key important variable. A functioning imperial peace, institutions supporting commerce and property that make it worthwhile to create and invest heavily in a sophisticated and productive division of labor, habits of mind and culture that reward cooperation and productivity instead of or even as well as domination—all of these can and do have profound influences on a society’s equilibrium capital intensity. In the Malthusian equilibrium of this model these factors affect population and population density, but surely there is feedback from capital intensity and population density to the economy’s tastes for luxuries as well.
Is this model I have set out a very powerful intuition pump? Is it merely a useful filing system? Is it a pointless scholastic exercise, leading to conclusions that any thinking human could have arrived at much more easily by other means? Is it a way of excluding people who do not have a certain particular familiarity with some kind of math from the discourse? Yes.
But I at least find it useful for making my major point: Our economic growth since 1870, and to some degree over 1770 to 1870, comes from breaking the Malthusian link between prosperity and population growth, first partially and now completely—the demographic transition and the rise of modern feminism, and the creation of a society in which durable female social power does not rely near-completely upon being the mother of surviving sons—and from the extraordinary waves of technological development. But previous “efflorescences”, in Jack Goldstone’s word, up to 1750 (and their inverse: collapses and dark ages) rely not on shifts in the technology growth rate hand feminist social revolutions, but instead on sociology, economics, and politics that produce durable alterations in '“subsistence” necessities consumption y^sub, the '“taste” for “luxuries” φ, and the creation and maintenance of imperial peace and other “inclusive” institutions that drive large shifts in s. Plus we then have the dynamics of convergence to a society’s Malthusian equilibrium from an initial state off of the equilibrium path.
I think a great deal is gained by calling such “efflorescences” and dark ages Malthusian, for I think they are, and that some insight is lost by rejecting the label.
That is obviously an economist's point of view, not a historians.
Historians have long noted a long term growth trend in European history. There were all sorts of innovations over the centuries: chimneys for heating, better plows on the Chinese model, shock absorbers for coaches, improved water wheels, better designed harnesses, flax culture and more effective yokes for animals. These led to an overall improvement in living standards and economic output. Advances rarely came alone. The introduction of the mechanical clock also marked a general improvements in making machinery which had further downstream effects.
Historians, particular those studying Europe, have noted a roughly two century cycle of economic expansion and contraction with the expansion associated with low but rising costs of food, fuel and rent and the contraction with extremely high costs of food, fuel and rent. These have been ascribed to Malthusian factors with the ratio of resources to population being an important driving factor of prices. There is also a cycle of urbanization. There are times when it is too dangerous to live far from a fortified urban center and more vulnerable farms are abandoned.
My feeling is that isn't really correct to call our current industrial regime non-Malthusian. We are much better at increasing productivity, industrial and agricultural, and much better at getting more efficient in our use of resources, but we are still resource limited. As Dyson pointed out, we are limited by the resources available to us as planets and lesser bodies in solar orbit and the energy output of our sun. At some extreme, we could rebuild our world as an optimal sphere, but then we'd hit a limit unless we were able to exploit other stars and their collections of miscellaneous matter.
It's not hard to imagine a world with ten billion people. It would look much like our current world but with more restrictions, fewer natural areas and a technology slightly more advanced than at present. If we consider a world with one hundred billion people, it quickly becomes obvious that such a world would require much more advanced technology and look quite different from the present. Current estimates of human use of the net planetary product run in the range of 20% to 50%, so increasing the population from 10^10 to 10^11 would require some major breakthroughs with regards to energy, water and agriculture and, at least during the transition stage, would entail rising prices for land, food and fuel much in the manner of earlier possibly Malthusian cycles.
We are already seeing Malthusian push back with regards to resources. Look at our periodic energy crises. Look at the more frequent conflicts with regards to harnessing fresh water sources. Look at the challenge of the Second Green Revolution and contemplate the likely necessary Third, Fourth, Fifth and so on. Whether you accept that humans are the cause of global warming and drying or not, there is still the fact of global warming and drying to deal with, and expecting that problem to just go away is not a realistic strategy.
We did have a major breakthrough with the Industrial Revolution, and it is likely the Romans had a similar major breakthrough that enabled their empire. We are either going to have to accept our Malthusian limits at some point or we are going to need another breakthrough, one that dwarfs that of the Industrial Revolution.
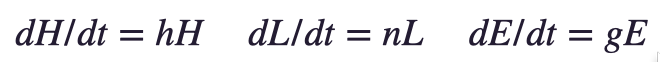
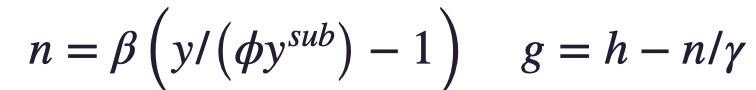
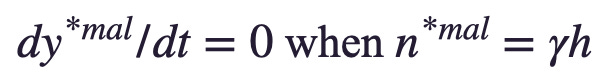
I like that, an appeal to mediocrity. (I had a roommate say that his tennis playing was fair with flashes of mediocrity.)
That is obviously an economist's point of view, not a historians.
Historians have long noted a long term growth trend in European history. There were all sorts of innovations over the centuries: chimneys for heating, better plows on the Chinese model, shock absorbers for coaches, improved water wheels, better designed harnesses, flax culture and more effective yokes for animals. These led to an overall improvement in living standards and economic output. Advances rarely came alone. The introduction of the mechanical clock also marked a general improvements in making machinery which had further downstream effects.
Historians, particular those studying Europe, have noted a roughly two century cycle of economic expansion and contraction with the expansion associated with low but rising costs of food, fuel and rent and the contraction with extremely high costs of food, fuel and rent. These have been ascribed to Malthusian factors with the ratio of resources to population being an important driving factor of prices. There is also a cycle of urbanization. There are times when it is too dangerous to live far from a fortified urban center and more vulnerable farms are abandoned.
My feeling is that isn't really correct to call our current industrial regime non-Malthusian. We are much better at increasing productivity, industrial and agricultural, and much better at getting more efficient in our use of resources, but we are still resource limited. As Dyson pointed out, we are limited by the resources available to us as planets and lesser bodies in solar orbit and the energy output of our sun. At some extreme, we could rebuild our world as an optimal sphere, but then we'd hit a limit unless we were able to exploit other stars and their collections of miscellaneous matter.
It's not hard to imagine a world with ten billion people. It would look much like our current world but with more restrictions, fewer natural areas and a technology slightly more advanced than at present. If we consider a world with one hundred billion people, it quickly becomes obvious that such a world would require much more advanced technology and look quite different from the present. Current estimates of human use of the net planetary product run in the range of 20% to 50%, so increasing the population from 10^10 to 10^11 would require some major breakthroughs with regards to energy, water and agriculture and, at least during the transition stage, would entail rising prices for land, food and fuel much in the manner of earlier possibly Malthusian cycles.
We are already seeing Malthusian push back with regards to resources. Look at our periodic energy crises. Look at the more frequent conflicts with regards to harnessing fresh water sources. Look at the challenge of the Second Green Revolution and contemplate the likely necessary Third, Fourth, Fifth and so on. Whether you accept that humans are the cause of global warming and drying or not, there is still the fact of global warming and drying to deal with, and expecting that problem to just go away is not a realistic strategy.
We did have a major breakthrough with the Industrial Revolution, and it is likely the Romans had a similar major breakthrough that enabled their empire. We are either going to have to accept our Malthusian limits at some point or we are going to need another breakthrough, one that dwarfs that of the Industrial Revolution.