There are Complex-Number One-Norm Square-Root of Probability Amplitudes of 0.006 in Which Sam Bankman-Fried Is Happy

Amplitudes in the quantum-mechanical superposition of the multiverse, that is. Getting philosophy-of-probability issues straight, and then deciding they are less important than issues of psychology...

Oct 05, 2023

Matt Levine thinks about Sam Bankman-Fried, risk-taking, and the Kelly Criterion—the rule that the fraction f of your wealth you should bet on a double-or-nothing bet is f = p - (1-p)/b, where p is the chance of winning and b is the win-loss odds ratio. (For more on that, I recommend William Poundstone: Fortune’s Formula.) Matt gets it mostly but, I think, not completely right:

Matt Levine: SBF Was Reckless From the Start: ‘People have thought about this question! Like, this is very much a central thing that traders and trading firms worry about. The standard starting point is the Kelly criterion, which computes a maximum bet size based on your edge and the size of your bankroll. Given the intern’s bankroll of $100, I think Kelly would tell you to put at most $10 on this bet…. I am being imprecise, and for various reasons you might not expect the interns to stick to Kelly in this situation. But when I read about interns lining up to lose their entire bankroll on bets with 1% edge, I think, “huh, that’s aggressive, what are they teaching those interns?”…
But I also think about a Twitter argument that Bankman-Fried had with Matt Hollerbach in 2020, in which Bankman-Fried scoffed at the Kelly criterion and said that “I, personally, would do more” than the Kelly amount. “Why? Because ultimately my utility function isn’t really logarithmic. It’s closer to linear.” As he tells Lewis, “he had use for ‘infinity dollars’”—he was going to become a trillionaire and use the money to cure disease and align AI and defeat Trump, sure—so he always wanted to maximize returns.
But… this misunderstands why trading firms use the Kelly criterion…. The point of Kelly is not about utility curves; it’s not “having $200 is less than twice as pleasant as having $100, so you should be less willing to take big risks for big rewards.” The point of Kelly is about maximizing your chances of surviving and obtaining long-run returns…. Kelly is about sizing your bets so you can keep playing the game and make the most money possible in the long run. Betting more can make you more money in the short run, but if you keep doing it you will end in ruin…

I think that the distinction Matt draws here is not quite right. It is about staying in the game to make positive-value bets in the future. But it is also about your utility value of $200 relative to $100.

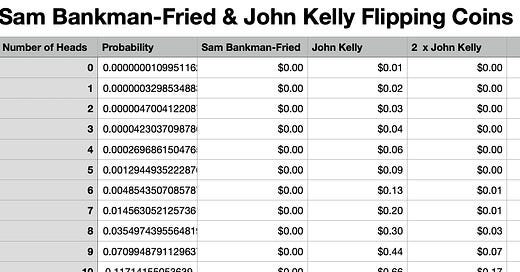
Suppose you start out with $1000 and have a sequence of sequence double-or-nothing bets, with the odds in your favor: a 60% chance you win, and a 40% chance you lose:

The Kelly criterion says: bet 20% of your current wealth each round.
Sam Bankman-Fried says: bet it all at each stage, and let it ride: <https://twitter.com/devahaz/status/1591908295312392193>.

After 20 bets, Sam Bankman-Fried is bankrupt 99.9963% of the time. But 0.0037% of the time he has $1,048,576,000. But his expected value is $38,340—19 million mosquito nets. 99.9963% of the time Sam Bankman-Fried has lost his dollar, and bought none of the mosquito nets he wanted to buy and distribute. But that 99.9963% of the time Sam Bankman-Fried consoles himself by thinking that somewhere out in the quantum superposition that is the multiverse is the version of him that got lucky and managed to buy and distribute 524,288,000 mosquito nets. And, if he is a good follower of the Everett interpretation of quantum mechanics, that makes Sam Bankman-Fried happy ex post. And there is the 0.0037% of the time that Sam Bankman Fried does manage to buy and distribute 524,288,000 mosquito nets,

After 20 bets, John Kelly has most likely gotten heads twelve times, and has turned his initial $1000 into $1500, with which he can buy 750 mosquito nets. 80% of the time his final wealth is between $440 and $5,050, buying between 220 and 2,525 mosquito nets. 10% of the time his wealth is lower; 10% of the time his wealth is higher. His expected wealth is $2,190—a little more than doubling his money, and enough to buy 1,095 mosquito nets. John Kelly is making an expected profit of only $1,190 because, at each stage, he is passing up 80% of his opportunity to make a positive expected-value bet.

Suppose that you were more aggressive than John Kelly—twice as aggressive, and bet 40% of your bankroll at each round. Then with your expected 12 heads you wind up with $950—losing $50. Why? Because each loss shrinks your bankroll to only 3/5 of what it had been, while each gain raises to only 7/5, and so each tails-heads round trip leaves you with only 21/25 of what you had and thus costs you 16% of your bankroll. This round-trip-hurts-you effect scales rapidly with the relative size of your bet: every single round trip wipes Sam Bankman-Fried out, but a round trip gives the original John Kelly fully 24/25 of his initial stake.

But the twice-as-aggressive-as-John-Kelly better does get an expected final wealth of $4,660, makes a profit of $3,660, and so can afford to buy 2330 mosquito nets. Only—60% of the time the malaria sufferers would have been better off if he had just bought 500 mosquito nets in the first place.

We have by now brushed by all of the deep philosophical and psychological issues in the study of probability, with the exception of two—two that are the most important of all:

What do we do with the fact that we are lousy at estimating probabilities, and lousier at actually acting according to their logic, even when we try to constrain ourselves with procedures and systems.
What does a Sam Bankman-Fried do when he first flips tails and goes bust? Does he say “oh well—it was a good try” and go do something else? Or does he break open the safe, grab the customers’ money, tell himself “I’m not really stealing it—I really will find a way to fudge the accounting and get it all back where it belongs after I flip my 20th head”, and place another bet? And so wind up in federal court on trial for embezzlement, whimpering “I never intended to keep the money but rather to pay it back”.

And indeed, trading firms use the Kelly criterion not so much because they have logarithmic utility functions but for three other reasons:

There is a value to the franchise from making future bets that is destroyed by bankruptcy, and that loss does not make it to the trader’s initial calculus.
If your traders do not believe what they are doing and not somewhat overestimate their chances of success, you probably do not have the right traders.
The psychological temptation when underwater to gamble-for-resurrection is very strong, and very human, and leads to true surprises as people discover who they really are and how many corners they are willing to cut.